Условие Куна-Таккера и уравнение Беллмана

Условие Куна-Таккера

Условие Куна-Таккера (или условия оптимальности в форме Куна-Таккера) является ключевым результатом в математической оптимизации, который используется для нахождения оптимального решения задачи оптимизации с ограничениями. Это условие было разработано Харольдом Куном, Фернандо Таккером и Робертом Карлсоном в 1950-х годах.

Условие Куна-Таккера формулируется для задач оптимизации с ограничениями типа равенств и неравенств. Оно утверждает, что если задача оптимизации удовлетворяет определенным условиям (например, выпуклости функций и ограничений), то существуют множители Лагранжа, которые могут быть использованы для нахождения оптимального решения.

Условие Куна-Таккера утверждает, что для точки, которая является локальным минимумом (или максимумом) функции с ограничениями, должны выполняться следующие условия:

1. Условия допустимости. Множители Лагранжа должны быть неотрицательными.

λ₁^*≥0, λ₂^*≥0,λ₃^*≥0,… λ_m^*≥0;

λ_i(x)≥0    i=1,m

2. Условие оптимальности. Градиент целевой функции должен быть пропорционален сумме градиентов ограничений с умноженными на множители Лагранжа.

 

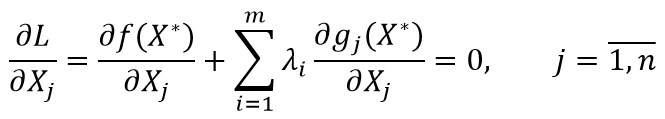
3. Условие трансверсальности. Если неравенственные ограничения активны, то соответствующие множители Лагранжа должны быть равны нулю

   

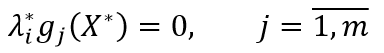
Теорема Куна-Таккера применяется для нахождения оптимума и достаточных условий оптимальности в задачах нелинейного программирования.

---

Уравнение Беллмана

Уравнение Беллмана — это ключевое понятие в теории динамического программирования и теории оптимального управления. Оно названо в честь американского математика Ричарда Беллмана, который внёс значительный вклад в развитие этих областей.

Уравнение Беллмана формулирует принцип оптимальности для многоразовых задач принятия решений в условиях неопределенности. Оно утверждает, что оптимальное решение задачи можно разбить на последовательность более простых решений, и оптимальное значение функции цели в каждой точке времени можно выразить через оптимальные значения функции цели в последующих точках времени.

В дискретном случае уравнение Беллмана для задачи динамического программирования имеет вид рекуррентного соотношения, которое связывает значение оптимальной функции цели в одной точке с значениями этой же функции в следующих точках времени. В непрерывном случае уравнение Беллмана может быть выражено в виде дифференциального уравнения.

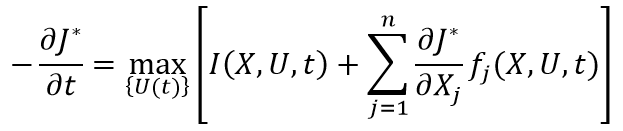
Ограничение на конечное состояние

J*(x(t),t)=F(x,t)