Разделим окружность на пять равных частей циркулем. Для начала начертим окружность. От центра окружности проведём два радиуса, перпендикулярные друг другу.
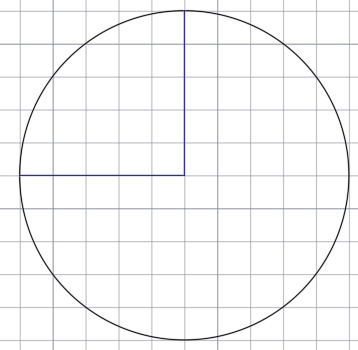
Чертим вспомогательную окружность с таким же радиусом, где центр новой окружности пересекается с точкой конца горизонтального радиуса данной окружности.
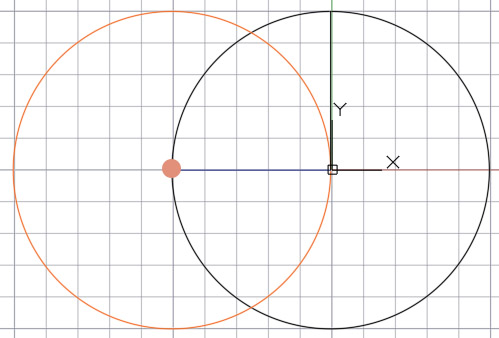
Далее, из точки пересечения двух окружностей — откладываем перпендикуляр на горизонтальный радиус окружности и в точке пересечения отмечаем точку.
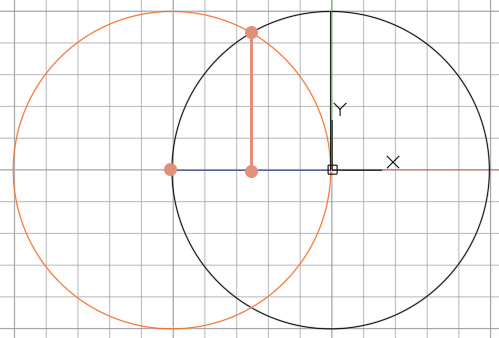
Из этой точки проводим отрезок к концу вертикального радиуса базовой окружности. Получившийся отрезок будет являться радиусом новой, дополнительной окружности. чертим дополнительную окружность зеленого цвета.
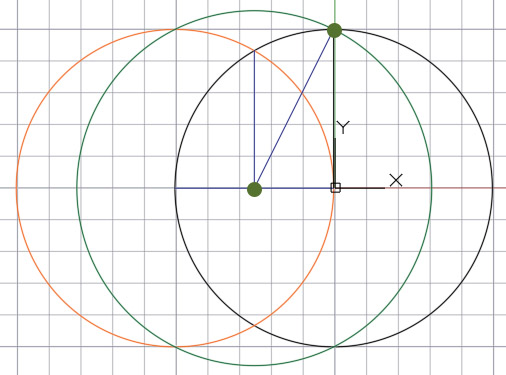
Из точки пересечения зеленой окружности и конца вертикального радиуса проводим отрезок в точку пересечения зеленой окружности с горизонтальным радиусом исходной окружности. Получившийся отрезок будет являться одной из сторон правильного пятиугольника. Откладываем данную длину циркулем по длине исходной окружности.
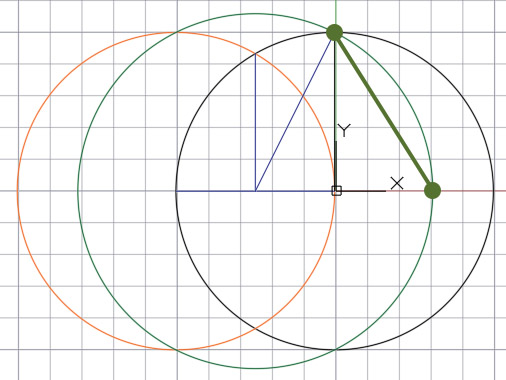
Соединяем точки вдоль основной окружности между собой. Получаем правильный равносторонний пятиугольник.
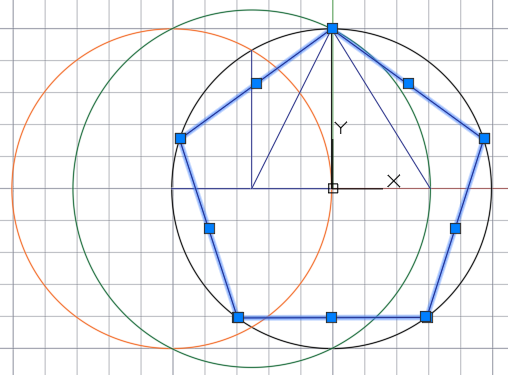
В итоги получаем пять точек. Соединяем точки с центром основной (базовой) окружности и таким образом делим окружность на 5 равных частей.
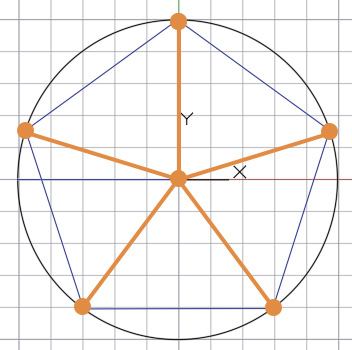
И таким образом получаем окружность окружность разделенную на 5 равных частей.
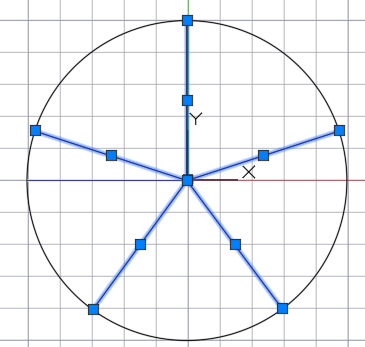
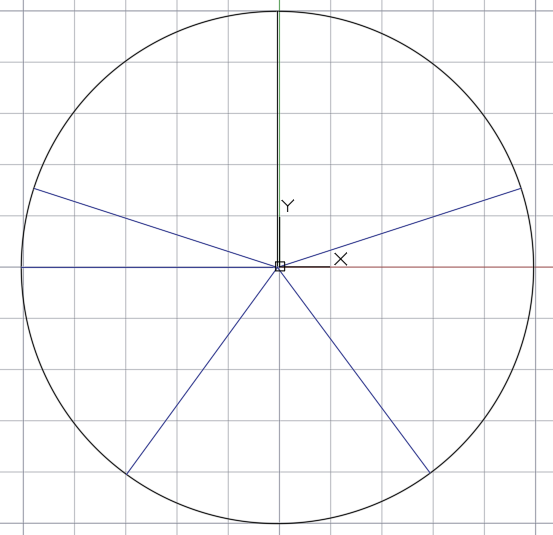

Части не равны!!! Способ ошибочный!
А вы можете точно написать значение числа пи?
Все исправили, спасибо вам!
Да, ну вы и математики… части не равные.
Спасибо вам за замечание. Статью полностью переработали и исправили. Приведенный метод деления окружности циркулем на 5 равных частей — здесь достаточно точный, проверен).