Однофакторный дисперсионный анализ изучает влияния одного фактора на анализируемый признак.
В таблицы приведены статистические данные по количеству изготовленных деталей на заводе каждым мастером в течение каждой недели.
Необходимо выяснить зависимость количества изготовленных деталей от производительности мастера. Уровень значимости равен α=0.05.
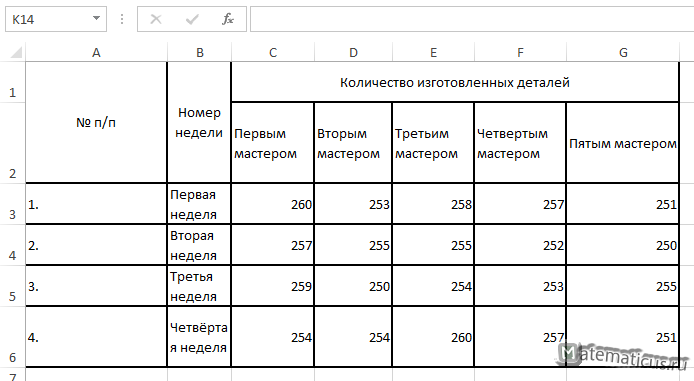
| № п/п | Номер недели | Количество изготовленных деталей | ||||
| Первым мастером | Вторым мастером | Третьим мастером | Четвертым мастером | Пятым мастером | ||
| 1. | Первая неделя | 260 | 253 | 258 | 257 | 251 |
| 2. | Вторая неделя | 257 | 255 | 255 | 252 | 250 |
| 3. | Третья неделя | 259 | 250 | 254 | 253 | 255 |
| 4. | Четвёртая неделя | 254 | 254 | 260 | 257 | 251 |
Решение
Переходим на вкладку Данные -> Анализ данных. Выбираем однофакторный дисперсионный анализ и жмём Ок.
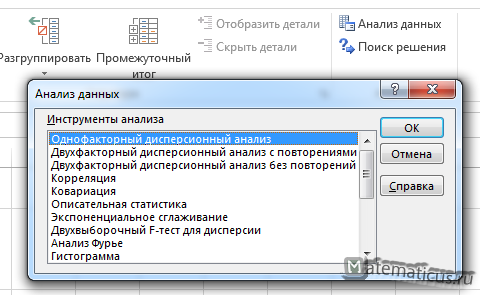
Появляется окно, здесь во входном интервале выбираем диапазон данный в нашей таблицы в нашем случае это диапазон ячеек $C$3:$G$6, альфа ставим 0,05 (обычно в Excel данная величина стоит по умолчанию) и в выходном интервале указываем произвольную ячейку на листе Excel, где желаете, чтобы отобразился результат, далее Ок.
В результате получим решение в виде таблицы.
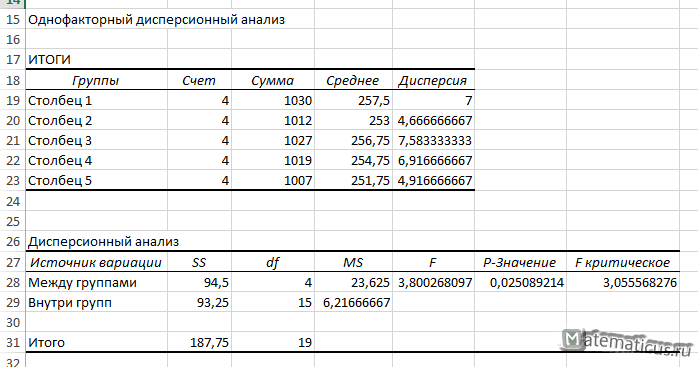
| Однофакторный дисперсионный анализ | ||||||
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| Столбец 1 | 4 | 1030 | 257,5 | 7 | ||
| Столбец 2 | 4 | 1012 | 253 | 4,666666667 | ||
| Столбец 3 | 4 | 1027 | 256,75 | 7,583333333 | ||
| Столбец 4 | 4 | 1019 | 254,75 | 6,916666667 | ||
| Столбец 5 | 4 | 1007 | 251,75 | 4,916666667 | ||
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 94,5 | 4 | 23,625 | 3,800268097 | 0,025089214 | 3,055568276 |
| Внутри групп | 93,25 | 15 | 6,21666667 | |||
| Итого | 187,75 | 19 | ||||
Из таблицы значения F-критерия равно Fнабл=3.8, а Fкрит=3, правосторонний интервал (3; +∞) Fнабл>Fкрит, отсюда следует, что Fнабл лежит в этом интервале, следовательно, нулевую гипотезу H0 о равенстве групповых матожиданий — отвергаем, следовательно фактор — количества изготовленных деталей зависит от признака — производительности мастера.
Найдём выборочный коэффициент детерминации:
${R^2} = \frac{{\frac{{94,5}}{{20}}}}{{\frac{{187,75}}{{20}}}} \approx 0,5$
Этот показатель говорит о том, что около половины еженедельного количества изготовленных деталей мастерами связано с номером недели.
