The distribution density of erlang’s law is defined by the expression:
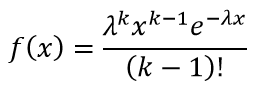
The mathematical expectation is determined by the formula:
$M(X) = \frac{k}{\lambda }$
The variance is equal to:
$D(X) = \frac{k}{{{\lambda ^2}}}$
Histogram of the erlang distribution for k=3 and λ=1:
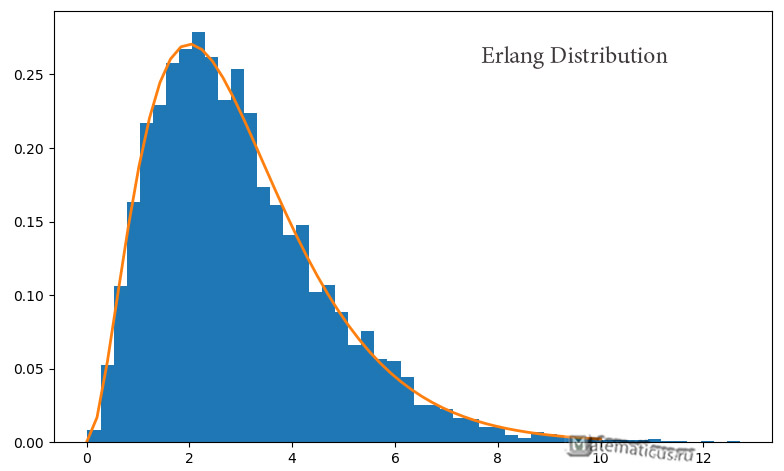
For k=1, the erlang distribution is converted to an exponential distribution with the parameter λ.
For k>1 and integer values of k, the gamma distribution is converted to the K-th order erlang distribution.
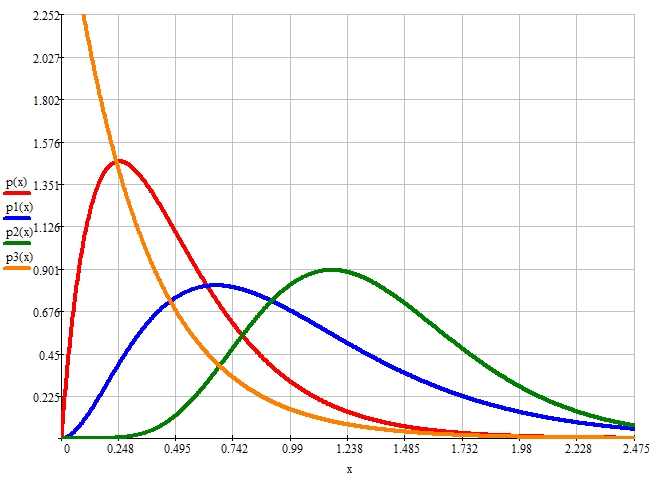
Plot of the distribution density of the erlang random variable at λ=4 and k=2, λ=3 and k=3, λ=6 and k=8, λ=3 and k=1
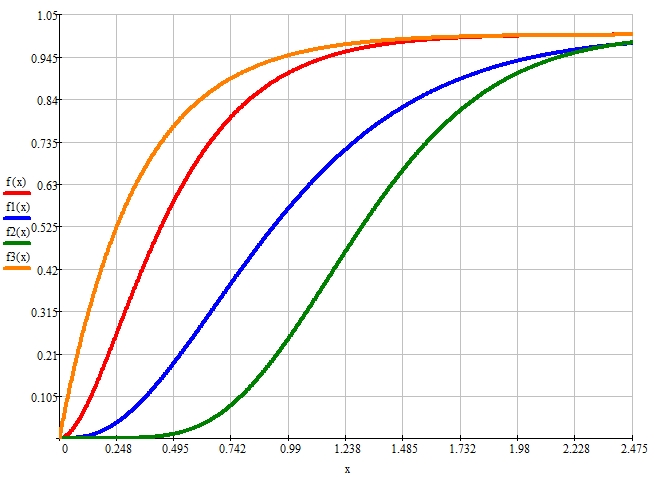
Plot of the distribution function of the erlang random variable for λ=4 and k=2, λ=3 and k=3, λ=6 and k=8, λ=3 and k=1
The erlang random variable distribution law is applied in the theory of Queuing, for example, the temporary downtime of public transport at stops, the moments when trucks arrive at the warehouse of building materials, etc.
