Алгоритм Беллмана Форда (нахождение кратчайшего расстояния между вершинами графа с отрицательными весами)
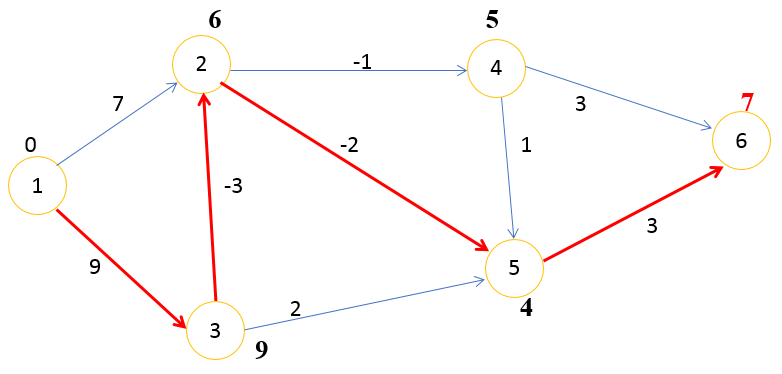
Для примера рассмотрим ориентированный граф с отрицательными весами вида:
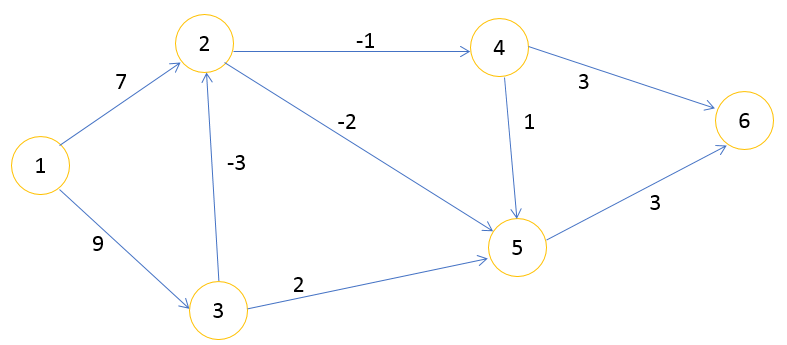
Требуется найти кратчайший путь из вершины 1 в вершину 6
Инициализируем граф, для этого начальной вершине графа присвоим значение нуля.
Оставшимся вершинам – бесконечно большое число ∞.
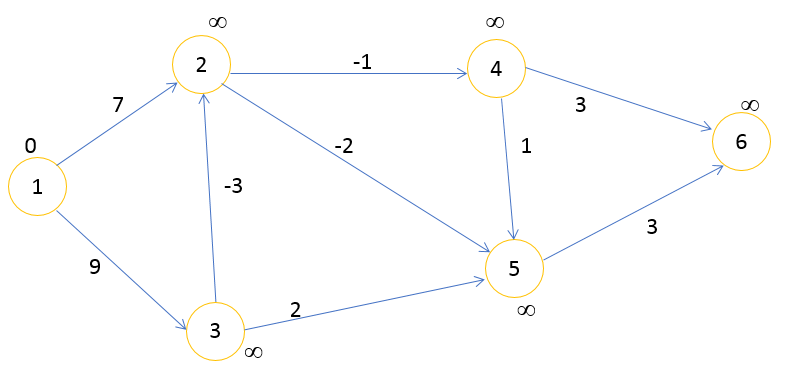
(1,2) (1,3) (2,4) (2,5) (3,2) (3,5) (4,5) (4,6) (5,6)
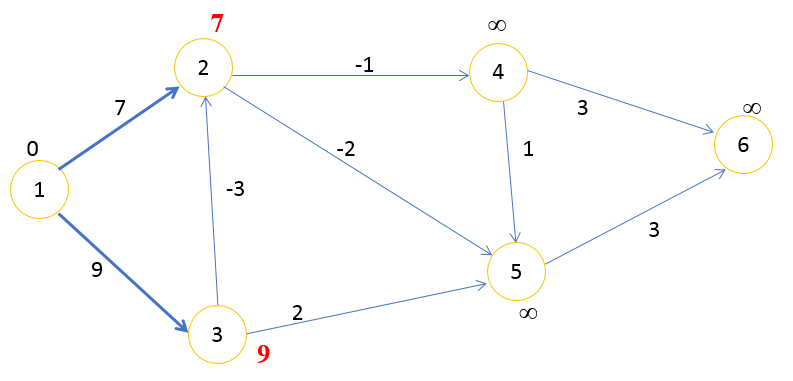
Первая итерация
Шаг 1
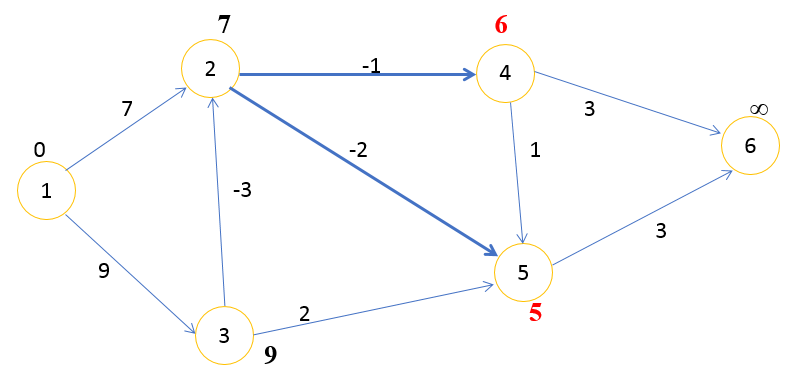
Шаг 2
Шаг 3
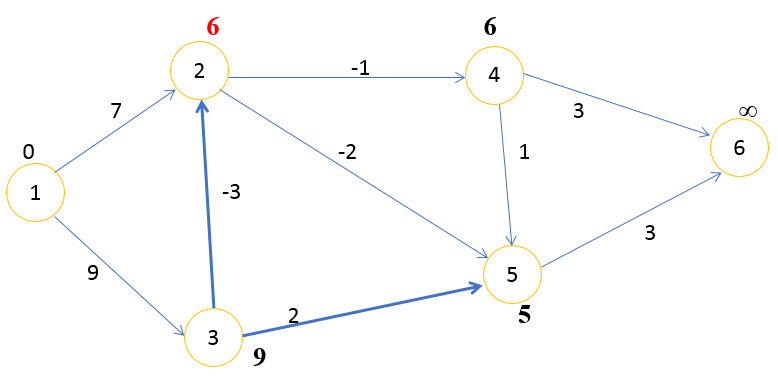
Шаг 4
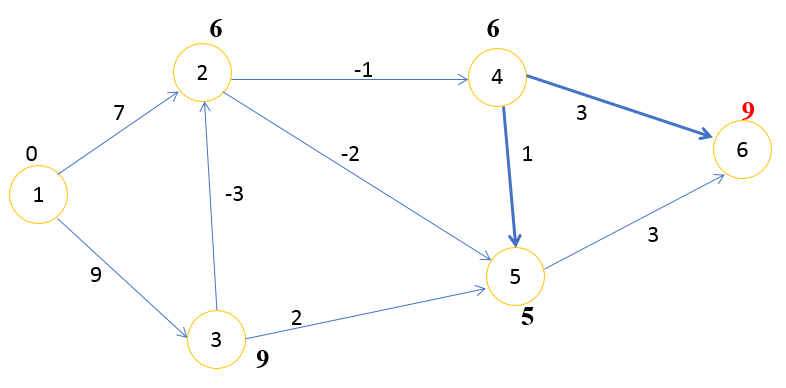
Шаг 5
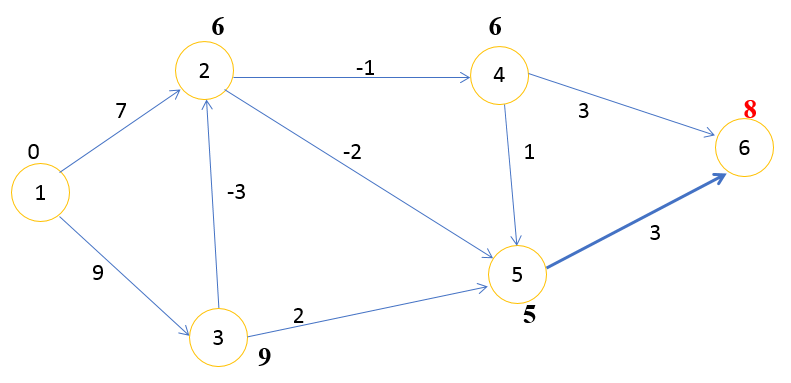
Вторая итерация
Шаг 1
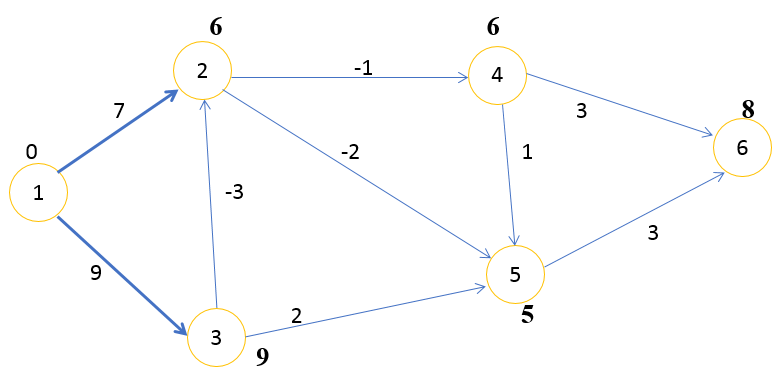
Шаг 2
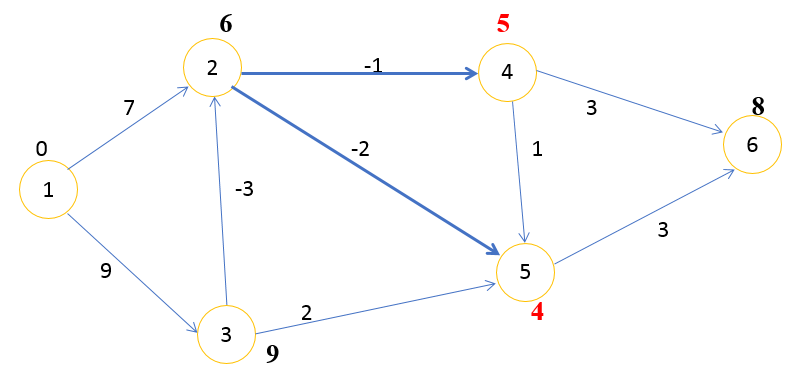
Шаг 3
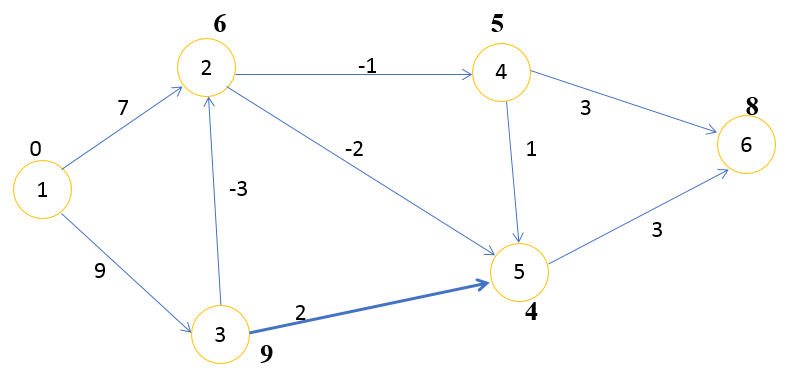
Шаг 4
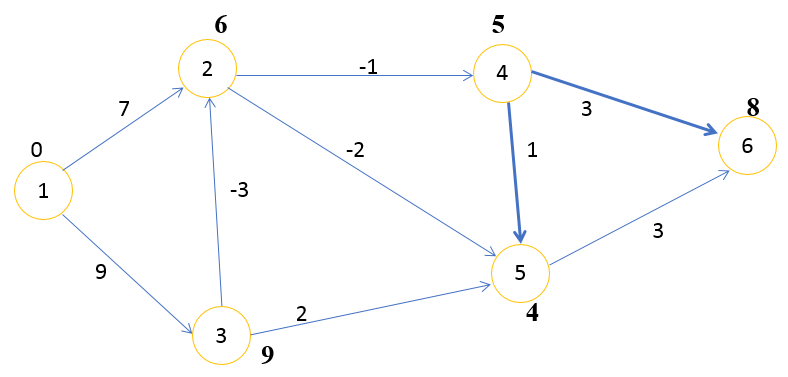
Шаг 5
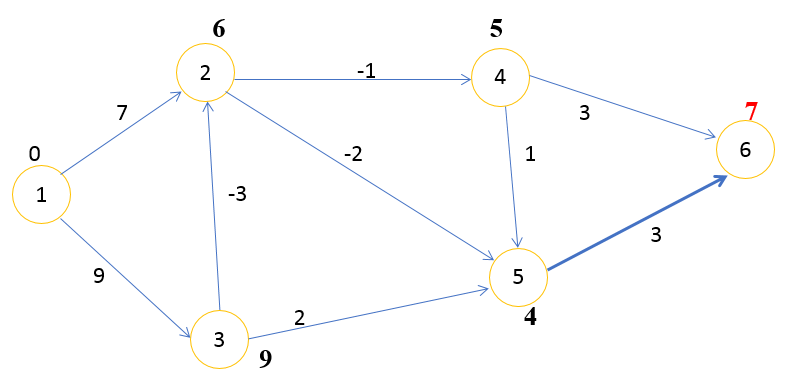
Аналогично проводим третью итерацию. В результате при расчёте расстояния остаются без изменений, следовательно, наилучший путь с помощью алгоритма Беллмана Форда найден и равен 7, то есть
1→3→2→5→6
if d[u]+s[u,v]<d[v] then d[v]=d[u]+s[u,v]
