Первый замечательный предел
Первый замечательный предел выражается формулой:
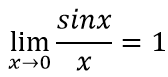
Следствием первого замечательного предела являются выражения:
$\underset{x\to 0}{\mathop{\lim }}\,\frac{tgx}{x}=1$
$\underset{x\to 0}{\mathop{\lim }}\,\frac{arcsinx}{x}=1$
$\underset{x\to 0}{\mathop{\lim }}\,\frac{arctgx}{x}=1$
Второй замечательный предел
Второй замечательный предел определяется из формулы:
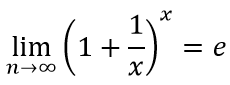
Следствием второго замечательного предела являются следующие математические зависимости:
$\underset{n\to \infty }{\mathop{\lim }}\,{{\left( 1+x \right)}^{\frac{1}{x}}}=e$
$\underset{n\to \infty }{\mathop{\lim }}\,{{\left( 1+\frac{k}{x} \right)}^{x}}={{e}^{k}}$
Второй замечательный предел используется для раскрытия неопределённости вида — 1∞.
Следствия замечательных пределов, формулы:
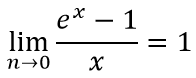
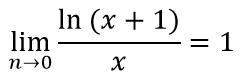
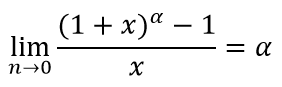
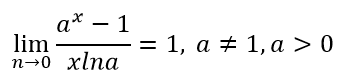
Пример 1 (первый замечательный предел)
$\underset{x\to 0}{\mathop{\lim }}\,\frac{1-\cos x}{{{x}^{2}}}=\left( \frac{0}{0} \right)=\underset{x\to 0}{\mathop{\lim }}\,\frac{2{{\sin }^{2}}\frac{x}{2}}{{{x}^{2}}}=\frac{1}{2}\underset{x\to 0}{\mathop{\lim }}\,{{\left( \frac{\sin \frac{x}{2}}{\frac{x}{2}} \right)}^{2}}=\frac{1}{2}\cdot 1=\frac{1}{2}$
Пример 2 (второй замечательный предел)
$\underset{x\ \to \,\infty }{\mathop{\lim }}\,\,\,{{\left( \,1+\frac{2}{x}\, \right)}^{x}}=\underset{x\ \to \,\infty }{\mathop{\lim }}\,\,\,{{\left( {{\left( \,1+\frac{2}{x}\, \right)}^{\frac{x}{2}}} \right)}^{2}}={{e}^{2}}$
