Интерполяция – это способ определения промежуточных значений по дискретному набору данных.
См. онлайн калькулятор линейная интерполяция.
Формула линейной интерполяции имеет вид:
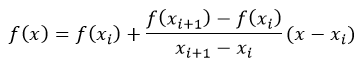
при
xi≤x≤xi+1
| x | f(x) |
| x1 | f(x1) |
| x | f(x) |
| x2 | f(x2) |
Ниже представлен график линейной интерполяции для нелинейной функции $y=\sqrt{x}$
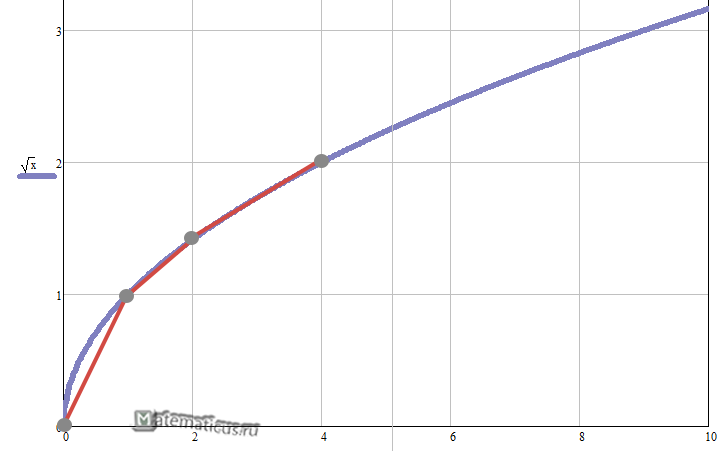
Пример 1
Воспользовавшись таблицей ниже, найдите неизвестное значение функции f(x) при x=3
| x | f(x) |
| 2 | 5 |
| 3 | ? |
| 5 | 11 |
Решение
Воспользуемся формулой линейной интерполяции, получим
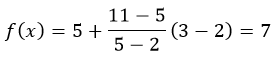
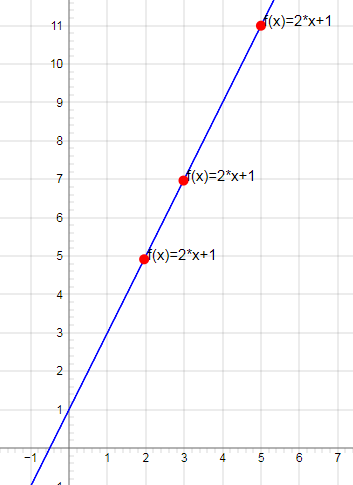
Так как данные в таблице представлены для линейной функция f(x)=2x+1. Для проверки полученного значения подставим в функцию значение X=3
f(3)=2*3+1=7
Пример 2
В соответствии с представленными данными в таблице, найдите неизвестное значение функции f(x) при x=3
| x | f(x) |
| 2 | 4 |
| 3 | ? |
| 5 | 25 |
Решение
Применим формулу линейной интерполяции, имеем
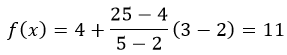
Так как данные в таблице представлены для нелинейной квадратной функции f(x)=x2. Проверим правильность, подставив в функцию значение X=3
f(3)=32=9
Значение получилось не совсем точное, так как метод линейной интерполяции применим в основном для линейных функций, а для нелинейных функций дает результаты с определенной погрешностью в зависимости от типа функции.

Было бы хорошо, если приведёте примеры с количеством чисел больше трёх.
По сути, далее не имеет значения, сколько чисел три, четыре и т.д. алгоритм тот же самый. Просто вы разбиваете функцию на несколько точек и последовательно их вычисляете с помощью данного метода.
это не линейная интерполяция. почему вы не рассказали про саму интерполяцию, т.е. нахождение прямой проходящей через кривую с минимальным среднекваратичным отклонением? все что показано это как найти у по х если функция задана таблично. нужен расчет а и в для у=ах+в. сам я расчет уже забыл и потерял, давно это было) думал в инете найти…
спутал, аппроксимация.) но такой на этом сайте не найдено…
Вот вам статьи, связанные с аппроксимацией
https://www.matematicus.ru/matematicheskaya-statistika/metod-naimenshih-kvadratov-regressiya
https://www.matematicus.ru/excel/regressionnaya-model-v-excel
А так, одно из главных отличий интерполяции от аппроксимации состоит в том, что аппроксимирующая функция не проходит через все узлы рассматриваемой функции, а лежит максимально близко к ним.