Длина вектора Расстояние между двумя точками в пространстве

Длина вектора в пространстве

Длиной (или модулем) вектора называется расстояние между началом и концом вектора.

Длина вектора a{X,Y,Z} выражается через его координаты следующей формулой:

Пример  
Длина вектора $a\left\{ { — 2,3,\sqrt 3 } \right\}$ равна

$\left| a \right| = \sqrt {{X^2} + {Y^2} + {Z^2}}  = $

$\sqrt {{{\left( { — 2} \right)}^2} + {3^2} + {{\left( {\sqrt 3 } \right)}^2}}  = \sqrt {16}  = 4$

Расстояние между двумя точками в пространстве

Расстояние d между точками в пространстве A₁{x₁;y₁;z₁}, A₂{x₂;y₂;z₂} представляется формулой

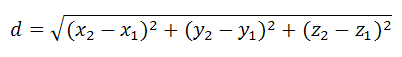
Пример 
Расстояние между точками A₁{4;-6;3} и A₂ {-1;5;-4}

$d = \sqrt {{{\left( {{x_2} — {x_1}} \right)}^2} + {{\left( {{y_2} — {y_1}} \right)}^2} + {{\left( {{z_2} — {z_1}} \right)}^2}} =  $

$=\sqrt {{{\left( { — 1 — 4} \right)}^2} + {{\left( {5 — \left( { — 6} \right)} \right)}^2} + {{\left( { — 4 — 3} \right)}^2}} =$

$  =\sqrt {25 + 121 + 49}  = \sqrt {195}  \approx 14$