Неравенство Чебышева

Закон больших чисел сформулирован Чебышевым в 1886 г.

Неравенство Чебышева (закон больших чисел) определяется по формуле:

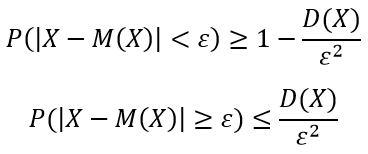
M(X) – математическое ожидание случайной величины X;
D(X) – дисперсия случайной величины X;
?>0

---

Пример
В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время Т лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время Т окажется: а) меньше трех; б) не меньше трех.

Решение
M(X)=n∙p=20∙0.8=16
D(X)=n∙p∙q=20∙0.8∙(1-0.8)=3.2
?=3
a)

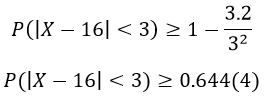
б)

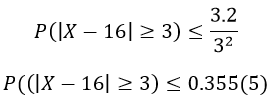
Так как события P(|X-16|<3) и P((|X-16|≥3) противоположны, отсюда следует, что сумма их вероятностей равна единице.