Метод Черчмена Акоффа или (метод последовательного сравнения) заключается в последовательной корректировке оценок. В методе последовательного сравнения, альтернативе a ставится действительное неотрицательное число (оценка) в диапазоне от 0 до 1, при этом, самой предпочтительной — первой альтернативе a1 оценка присваивается максимальная, то есть 1, остальным ниже 1 (но на практике не всегда так бывает).
Математически, это можно записать в следующем виде:

в ином случае формула имеет вид
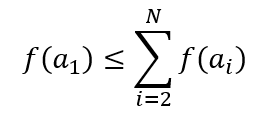
Из этого можно сделать вывод, что первая альтернатива должна быть наиболее предпочтительна, чем сумма альтернатив
a2+a3+…+aN
Если условие выполняется, то первую альтернативу условно исключаем, и за основную берём вторую альтернативу, оценка которой должна быть больше суммы оставшихся альтернатив
a3+a4+…+aN
Проделываем это до тех пор, пока не останется альтернатив.
Пример
Имеется четыре альтернативы, которые проранжированы следующим образом:
a1>a2>a3>a4
Проведём оценку альтернатив от 0 до 1
Получили соответствующие оценки
| a1 | a2 | a3 | a4 |
| 1 | 0,7 | 0,5 | 0,1 |
Преминем метод Черчмена Акоффа для корректирования оценок экспертов и в итоги должны получить следующий результат
a1>(a2+a3+a4)
1,4>(0,7+0,5+0,1)
0,7>(0,5+0,1)
0,5>0,1
Суммарная оценка равна 2,5.
В итоги получаем нормированные значения оценок
| a1 | a2 | a3 | a4 |
| 0,56 | 0,28 | 0,2 | 0,04 |
