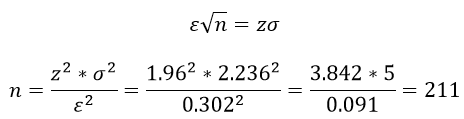Оценка доверительного интервала нормального закона распределения определяется по формуле:
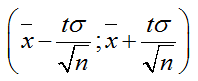
Значение t определяется из выражения 2Φ(t)=γ, где Φ(t) — функция Лапласа (определяется по таблице)
${\overline x }$ — среднее значение
Пример 1
Диаметр вала, изготавливаемого на данном станке, представляет собой случайную величину, распределенную по нормальному закону со среднеквадратическим отклонением З мм. Для проверки качества продукции отобрано 9 изделий. Найти доверительный интервал надежности 95% для среднего значения диаметра вала, если для отобранных изделий средний диаметр оказался равным 30 мм.
Решение
2Φ(t)=0.95 ⇒Φ(t)=0.475
По таблице значений функции Лапласа t=1.96
Тогда доверительный интервал нормального закона распределения равен:
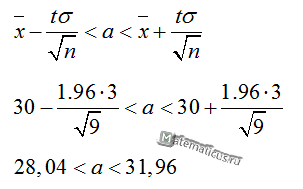
Пример 2
Известно, что $x̃=-8, s^2=5, n=180, N=5000$. Найти границы, в которых с вероятностью γ=0.93 заключено генеральное среднее? Сколько элементов надо взять , чтобы те же границы гарантировать с вероятностью 0.95?
Решение
Дано
$x̃=-8, s^2=5 (σ=\sqrt{5}=2.236),n=180, N=5000, γ=0.93$
Из равенства по таблице значений интегральных функций Лапласа находим
$z=1.81$
Откуда находим
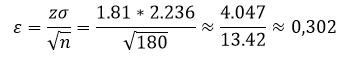
Таким образом получаем границы данной вероятности
$-8-0.302<N<-8+0.302$
$-8.302<N<-7.698$
Далее, cколько элементов надо взять , чтобы те же границы гарантировать с вероятностью 0.93? из равенства
$P=2Φ(z)=0.95$
$P=Φ(z)=0.475$
по таблице значений интегральных функций Лапласа находим
$z= 1.96$