Алгоритм Дейкстры — нахождения кратчайшего пути

Алгоритм Дейкстры (нахождение кратчайшего расстояния между вершинами графа)

В качестве примера решения алгоритма Дейкстры

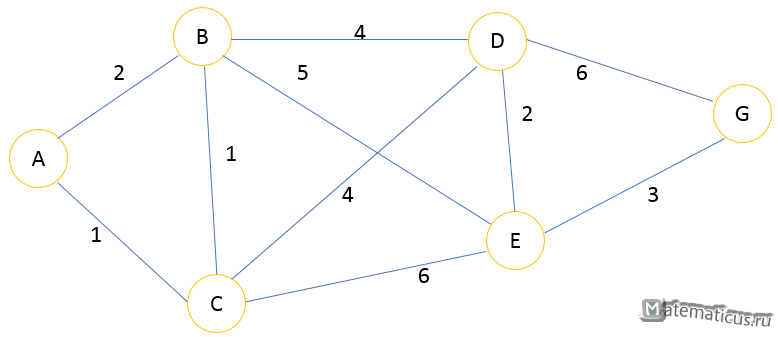
Пусть дан граф 

Необходимо найти кратчайший путь из вершины A в вершину G

Решение

Приведём его к виду

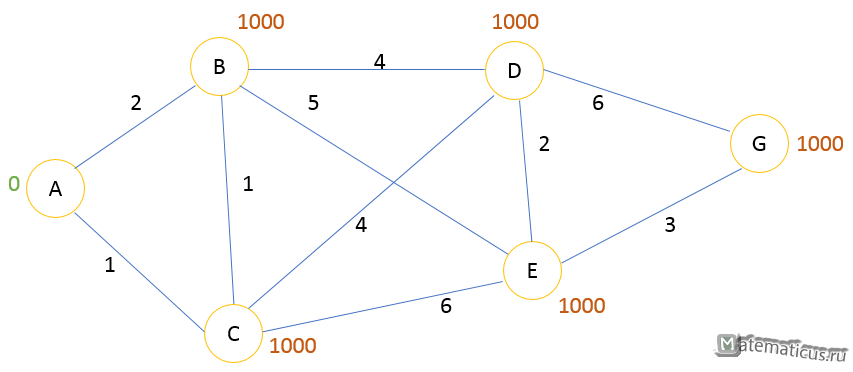
Инициализация графа

Начальной вершине графа присвоим значение 0, A=0

Оставшимся вершинам присваиваем значение с большим числом, пусть в данном случае будет 1000 (∞).

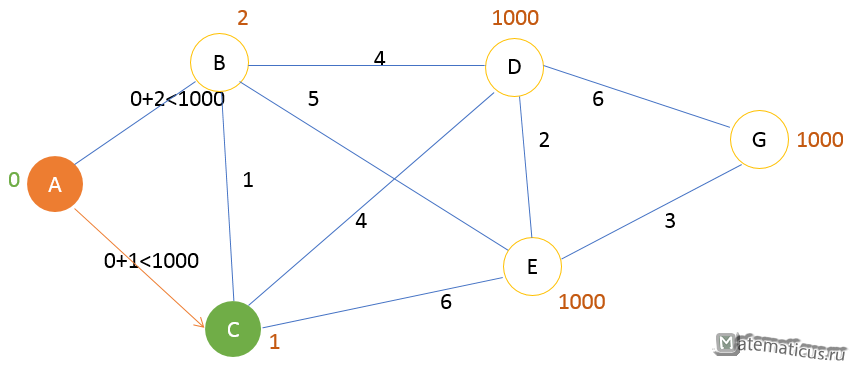
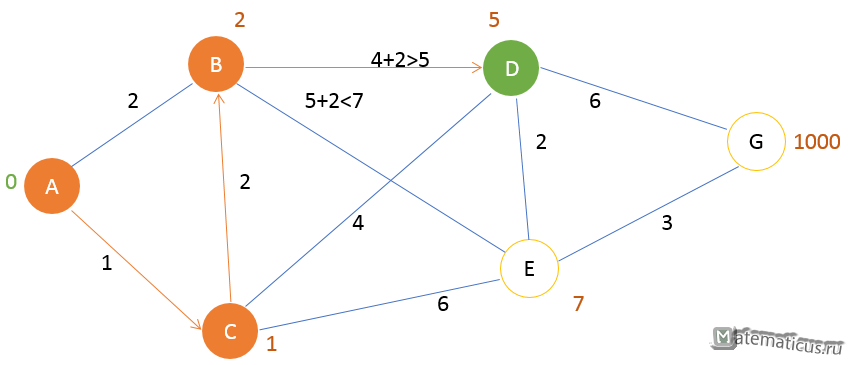
Шаг 1

Соседними вершинами A являются вершины C и B. Сначала посещаем вершину с минимальным путем – вершину C и помечаем её как текущую метку, затем по убыванию остальные вершины, в данном случае вершину B. Вершину A помечаем как посещённую.

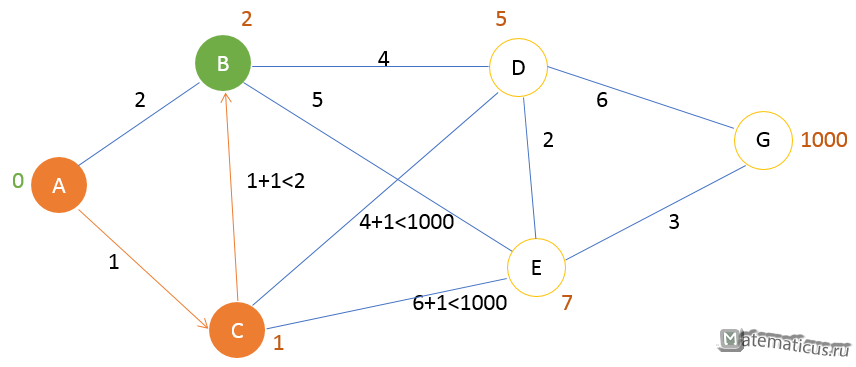
Шаг 2

Соседними вершинами С являются вершины B,D и E.  Посещаем вершину с наименьшем путем – вершину B и помечаем её как текущую метку, затем оставшиеся вершины — вершину D и E. Вершину С помечаем как посещённую.

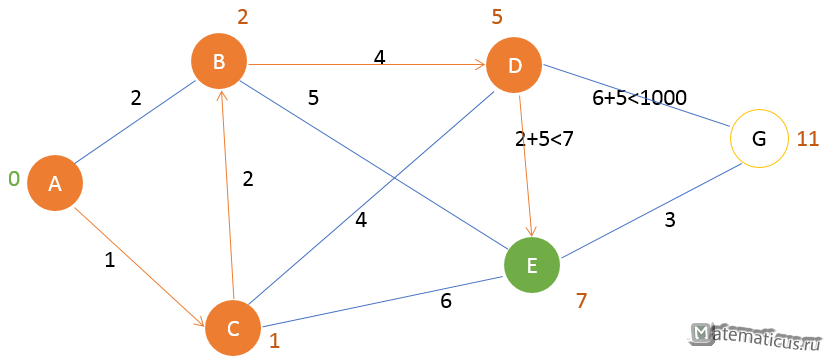
Шаг 3

Соседними вершинами B — вершина D и E.  Посещаем вершину с наименьшем путем – вершину D и помечаем её как текущую метку, затем вершину E. Вершину B помечаем как посещённую.

Шаг 4

Соседние вершины D — вершина G и E.  Посещаем вершину с наименьшем путем – вершину E и помечаем её как текущую метку, затем вершину G. Вершину D помечаем как посещённую.

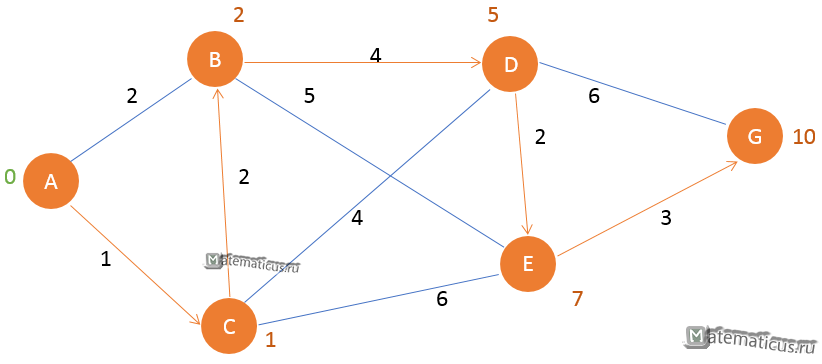
Шаг 5

Соседней вершиной E является оставшиеся последняя вершина G.  Посещаем вершину G и помечаем как посещённую. На этом алгоритм заканчивается.

Итак, самый короткий маршрут получился A C B D E G и равен 10.

Таким образом, оптимальный путь алгоритм Дейкстры определяется выражением

if d[u]>d[v]+c[v,u] then 

d[u]=d[v]+c[v,u]

p[u]=(p[v],u)

u — посещенная вершина графа;

v — текущая вершина графа;

d[u] — длина кратчайшего пути до вершины v, минимальное расстояние;

p[u] — список посещенных вершин;

c[i,j] — вес ребра;

Сложность алгоритма: O(n²)

С применением двоичной кучи сложность алгоритма равна: O(log n*(n+m))

Алгоритм Дейкстры (Dijkstra’s Algorithm) открыт в 1959 году Эдсгером Дейкстрой.